deep learning 作業 2.2

阅读量：5990 次

发布时间：2019-06-20

本文共 39951 字，大约阅读时间需要 133 分钟。

Optimization Methods

Until now, you've always used Gradient Descent to update the parameters and minimize the cost. In this notebook, you will learn more advanced optimization methods that can speed up learning and perhaps even get you to a better final value for the cost function. Having a good optimization algorithm can be the difference between waiting days vs. just a few hours to get a good result.

Gradient descent goes "downhill" on a cost function JJ. Think of it as trying to do this:

**Figure 1** : **Minimizing the cost is like finding the lowest point in a hilly landscape**

At each step of the training, you update your parameters following a certain direction to try to get to the lowest possible point.

Notations: As usual, ∂J∂a=∂J∂a= da for any variable a.

To get started, run the following code to import the libraries you will need.

In [1]:

import numpy as npimport matplotlib.pyplot as pltimport scipy.ioimport mathimport sklearnimport sklearn.datasetsfrom opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagationfrom opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_datasetfrom testCases import *%matplotlib inlineplt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plotsplt.rcParams['image.interpolation'] = 'nearest'plt.rcParams['image.cmap'] = 'gray'

1 - Gradient Descent

A simple optimization method in machine learning is gradient descent (GD). When you take gradient steps with respect to all mm examples on each step, it is also called Batch Gradient Descent.

Warm-up exercise: Implement the gradient descent update rule. The gradient descent rule is, for l=1,...,Ll=1,...,L:

W[l]=W[l]−α dW[l](1)(1)W[l]=W[l]−α dW[l]

b[l]=b[l]−α db[l](2)(2)b[l]=b[l]−α db[l]

where L is the number of layers and αα is the learning rate. All parameters should be stored in the parameters dictionary. Note that the iterator l starts at 0 in the for loop while the first parameters are W[1]W[1] and b[1]b[1]. You need to shift l to l+1 when coding.

In [2]:

# GRADED FUNCTION: update_parameters_with_gddef update_parameters_with_gd(parameters, grads, learning_rate):    """    Update parameters using one step of gradient descent        Arguments:    parameters -- python dictionary containing your parameters to be updated:                    parameters['W' + str(l)] = Wl                    parameters['b' + str(l)] = bl    grads -- python dictionary containing your gradients to update each parameters:                    grads['dW' + str(l)] = dWl                    grads['db' + str(l)] = dbl    learning_rate -- the learning rate, scalar.        Returns:    parameters -- python dictionary containing your updated parameters     """    L = len(parameters) // 2 # number of layers in the neural networks    # Update rule for each parameter    for l in range(L):        ### START CODE HERE ### (approx. 2 lines)        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads['dW' + str(l+1)]        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads['db' + str(l+1)]        ### END CODE HERE ###            return parameters

In [3]:

parameters, grads, learning_rate = update_parameters_with_gd_test_case()parameters = update_parameters_with_gd(parameters, grads, learning_rate)print("W1 = " + str(parameters["W1"]))print("b1 = " + str(parameters["b1"]))print("W2 = " + str(parameters["W2"]))print("b2 = " + str(parameters["b2"]))

W1 = [[ 1.63535156 -0.62320365 -0.53718766] [-1.07799357  0.85639907 -2.29470142]]b1 = [[ 1.74604067] [-0.75184921]]W2 = [[ 0.32171798 -0.25467393  1.46902454] [-2.05617317 -0.31554548 -0.3756023 ] [ 1.1404819  -1.09976462 -0.1612551 ]]b2 = [[-0.88020257] [ 0.02561572] [ 0.57539477]]

Expected Output:

W1	[[ 1.63535156 -0.62320365 -0.53718766] [-1.07799357 0.85639907 -2.29470142]]
b1	[[ 1.74604067] [-0.75184921]]
W2	[[ 0.32171798 -0.25467393 1.46902454] [-2.05617317 -0.31554548 -0.3756023 ] [ 1.1404819 -1.09976462 -0.1612551 ]]
b2	[[-0.88020257] [ 0.02561572] [ 0.57539477]]

A variant of this is Stochastic Gradient Descent (SGD), which is equivalent to mini-batch gradient descent where each mini-batch has just 1 example. The update rule that you have just implemented does not change. What changes is that you would be computing gradients on just one training example at a time, rather than on the whole training set. The code examples below illustrate the difference between stochastic gradient descent and (batch) gradient descent.

(Batch) Gradient Descent:

X = data_inputY = labelsparameters = initialize_parameters(layers_dims)for i in range(0, num_iterations):    # Forward propagation    a, caches = forward_propagation(X, parameters)    # Compute cost.    cost = compute_cost(a, Y)    # Backward propagation.    grads = backward_propagation(a, caches, parameters)    # Update parameters.    parameters = update_parameters(parameters, grads)

Stochastic Gradient Descent:

X = data_inputY = labelsparameters = initialize_parameters(layers_dims)for i in range(0, num_iterations):    for j in range(0, m):        # Forward propagation        a, caches = forward_propagation(X[:,j], parameters)        # Compute cost        cost = compute_cost(a, Y[:,j])        # Backward propagation        grads = backward_propagation(a, caches, parameters)        # Update parameters.        parameters = update_parameters(parameters, grads)

In Stochastic Gradient Descent, you use only 1 training example before updating the gradients. When the training set is large, SGD can be faster. But the parameters will "oscillate" toward the minimum rather than converge smoothly. Here is an illustration of this:

**Figure 1** : **SGD vs GD**

"+" denotes a minimum of the cost. SGD leads to many oscillations to reach convergence. But each step is a lot faster to compute for SGD than for GD, as it uses only one training example (vs. the whole batch for GD).

Note also that implementing SGD requires 3 for-loops in total:

Over the number of iterations

Over the mm training examples

Over the layers (to update all parameters, from (W[1],b[1])(W[1],b[1]) to (W[L],b[L])(W[L],b[L]))

In practice, you'll often get faster results if you do not use neither the whole training set, nor only one training example, to perform each update. Mini-batch gradient descent uses an intermediate number of examples for each step. With mini-batch gradient descent, you loop over the mini-batches instead of looping over individual training examples.

**Figure 2** : **SGD vs Mini-Batch GD**

"+" denotes a minimum of the cost. Using mini-batches in your optimization algorithm often leads to faster optimization.

What you should remember:

The difference between gradient descent, mini-batch gradient descent and stochastic gradient descent is the number of examples you use to perform one update step.

You have to tune a learning rate hyperparameter αα.

With a well-turned mini-batch size, usually it outperforms either gradient descent or stochastic gradient descent (particularly when the training set is large).

2 - Mini-Batch Gradient descent

Let's learn how to build mini-batches from the training set (X, Y).

There are two steps:

Shuffle: Create a shuffled version of the training set (X, Y) as shown below. Each column of X and Y represents a training example. Note that the random shuffling is done synchronously between X and Y. Such that after the shuffling the ithith column of X is the example corresponding to the ithithlabel in Y. The shuffling step ensures that examples will be split randomly into different mini-batches.

Partition: Partition the shuffled (X, Y) into mini-batches of size mini_batch_size (here 64). Note that the number of training examples is not always divisible by mini_batch_size. The last mini batch might be smaller, but you don't need to worry about this. When the final mini-batch is smaller than the full mini_batch_size, it will look like this:

Exercise: Implement random_mini_batches. We coded the shuffling part for you. To help you with the partitioning step, we give you the following code that selects the indexes for the 1st1st and 2nd2nd mini-batches:

first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]...

Note that the last mini-batch might end up smaller than mini_batch_size=64. Let ⌊s⌋⌊s⌋ represents ss rounded down to the nearest integer (this is math.floor(s) in Python). If the total number of examples is not a multiple of mini_batch_size=64 then there will be ⌊mmini_batch_size⌋⌊mmini_batch_size⌋ mini-batches with a full 64 examples, and the number of examples in the final mini-batch will be (m−mini_batch_size×⌊mmini_batch_size⌋m−mini_batch_size×⌊mmini_batch_size⌋).

In [4]:

# GRADED FUNCTION: random_mini_batchesdef random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):    """    Creates a list of random minibatches from (X, Y)        Arguments:    X -- input data, of shape (input size, number of examples)    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)    mini_batch_size -- size of the mini-batches, integer        Returns:    mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)    """        np.random.seed(seed)            # To make your "random" minibatches the same as ours    m = X.shape[1]                  # number of training examples    mini_batches = []            # Step 1: Shuffle (X, Y)    permutation = list(np.random.permutation(m))    shuffled_X = X[:, permutation]    shuffled_Y = Y[:, permutation].reshape((1,m))    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning    for k in range(0, num_complete_minibatches):        ### START CODE HERE ### (approx. 2 lines)        mini_batch_X = shuffled_X[:, k*mini_batch_size : (k+1) * mini_batch_size]        mini_batch_Y = shuffled_Y[:, k*mini_batch_size : (k+1) * mini_batch_size]        ### END CODE HERE ###        mini_batch = (mini_batch_X, mini_batch_Y)        mini_batches.append(mini_batch)        # Handling the end case (last mini-batch < mini_batch_size)    if m % mini_batch_size != 0:        ### START CODE HERE ### (approx. 2 lines)        mini_batch_X = shuffled_X[:, num_complete_minibatches*mini_batch_size:]        mini_batch_Y = shuffled_Y[:, num_complete_minibatches*mini_batch_size:]        ### END CODE HERE ###        mini_batch = (mini_batch_X, mini_batch_Y)        mini_batches.append(mini_batch)        return mini_batches

In [5]:

X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape)) print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))

shape of the 1st mini_batch_X: (12288, 64)shape of the 2nd mini_batch_X: (12288, 64)shape of the 3rd mini_batch_X: (12288, 20)shape of the 1st mini_batch_Y: (1, 64)shape of the 2nd mini_batch_Y: (1, 64)shape of the 3rd mini_batch_Y: (1, 20)mini batch sanity check: [ 0.90085595 -0.7612069   0.2344157 ]

Expected Output:

shape of the 1st mini_batch_X	(12288, 64)
shape of the 2nd mini_batch_X	(12288, 64)
shape of the 3rd mini_batch_X	(12288, 20)
shape of the 1st mini_batch_Y	(1, 64)
shape of the 2nd mini_batch_Y	(1, 64)
shape of the 3rd mini_batch_Y	(1, 20)
mini batch sanity check	[ 0.90085595 -0.7612069 0.2344157 ]

What you should remember:

Shuffling and Partitioning are the two steps required to build mini-batches

Powers of two are often chosen to be the mini-batch size, e.g., 16, 32, 64, 128.

3 - Momentum

Because mini-batch gradient descent makes a parameter update after seeing just a subset of examples, the direction of the update has some variance, and so the path taken by mini-batch gradient descent will "oscillate" toward convergence. Using momentum can reduce these oscillations.

Momentum takes into account the past gradients to smooth out the update. We will store the 'direction' of the previous gradients in the variable vv. Formally, this will be the exponentially weighted average of the gradient on previous steps. You can also think of vv as the "velocity" of a ball rolling downhill, building up speed (and momentum) according to the direction of the gradient/slope of the hill.

**Figure 3**: The red arrows shows the direction taken by one step of mini-batch gradient descent with momentum. The blue points show the direction of the gradient (with respect to the current mini-batch) on each step. Rather than just following the gradient, we let the gradient influence vv and then take a step in the direction of vv.

Exercise: Initialize the velocity. The velocity, vv, is a python dictionary that needs to be initialized with arrays of zeros. Its keys are the same as those in the grads dictionary, that is: for l=1,...,Ll=1,...,L:

v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])

Note that the iterator l starts at 0 in the for loop while the first parameters are v["dW1"] and v["db1"] (that's a "one" on the superscript). This is why we are shifting l to l+1 in the for loop.

In [6]:

# GRADED FUNCTION: initialize_velocitydef initialize_velocity(parameters):    """    Initializes the velocity as a python dictionary with:                - keys: "dW1", "db1", ..., "dWL", "dbL"                 - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.    Arguments:    parameters -- python dictionary containing your parameters.                    parameters['W' + str(l)] = Wl                    parameters['b' + str(l)] = bl        Returns:    v -- python dictionary containing the current velocity.                    v['dW' + str(l)] = velocity of dWl                    v['db' + str(l)] = velocity of dbl    """        L = len(parameters) // 2 # number of layers in the neural networks    v = {}        # Initialize velocity    for l in range(L):        ### START CODE HERE ### (approx. 2 lines)        v["dW" + str(l+1)] = np.zeros((parameters["W" + str(l+1)].shape))        v["db" + str(l+1)] = np.zeros((parameters["b" + str(l+1)].shape))        ### END CODE HERE ###            return v

In [7]:

parameters = initialize_velocity_test_case()v = initialize_velocity(parameters)print("v[\"dW1\"] = " + str(v["dW1"]))print("v[\"db1\"] = " + str(v["db1"]))print("v[\"dW2\"] = " + str(v["dW2"]))print("v[\"db2\"] = " + str(v["db2"]))

v["dW1"] = [[ 0.  0.  0.] [ 0.  0.  0.]]v["db1"] = [[ 0.] [ 0.]]v["dW2"] = [[ 0.  0.  0.] [ 0.  0.  0.] [ 0.  0.  0.]]v["db2"] = [[ 0.] [ 0.] [ 0.]]

Expected Output:

v["dW1"]	[[ 0. 0. 0.] [ 0. 0. 0.]]
v["db1"]	[[ 0.] [ 0.]]
v["dW2"]	[[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
v["db2"]	[[ 0.] [ 0.] [ 0.]]

Exercise: Now, implement the parameters update with momentum. The momentum update rule is, for l=1,...,Ll=1,...,L:

{vdW[l]=βvdW[l]+(1−β)dW[l]W[l]=W[l]−αvdW[l](3)(3){vdW[l]=βvdW[l]+(1−β)dW[l]W[l]=W[l]−αvdW[l]

{vdb[l]=βvdb[l]+(1−β)db[l]b[l]=b[l]−αvdb[l](4)(4){vdb[l]=βvdb[l]+(1−β)db[l]b[l]=b[l]−αvdb[l]

where L is the number of layers, ββ is the momentum and αα is the learning rate. All parameters should be stored in the parameters dictionary. Note that the iterator l starts at 0 in the for loop while the first parameters are W[1]W[1] and b[1]b[1] (that's a "one" on the superscript). So you will need to shift l to l+1 when coding.

In [8]:

# GRADED FUNCTION: update_parameters_with_momentumdef update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):    """    Update parameters using Momentum        Arguments:    parameters -- python dictionary containing your parameters:                    parameters['W' + str(l)] = Wl                    parameters['b' + str(l)] = bl    grads -- python dictionary containing your gradients for each parameters:                    grads['dW' + str(l)] = dWl                    grads['db' + str(l)] = dbl    v -- python dictionary containing the current velocity:                    v['dW' + str(l)] = ...                    v['db' + str(l)] = ...    beta -- the momentum hyperparameter, scalar    learning_rate -- the learning rate, scalar        Returns:    parameters -- python dictionary containing your updated parameters     v -- python dictionary containing your updated velocities    """    L = len(parameters) // 2 # number of layers in the neural networks        # Momentum update for each parameter    for l in range(L):                ### START CODE HERE ### (approx. 4 lines)        # compute velocities        v["dW" + str(l+1)] = beta*v["dW" + str(l+1)] + (1-beta)*grads['dW' + str(l+1)]        v["db" + str(l+1)] = beta*v["db" + str(l+1)] + (1-beta)*grads['db' + str(l+1)]        # update parameters        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]        ### END CODE HERE ###            return parameters, v

In [9]:

parameters, grads, v = update_parameters_with_momentum_test_case()parameters, v = update_parameters_with_momentum(parameters, grads, v, beta = 0.9, learning_rate = 0.01)print("W1 = " + str(parameters["W1"]))print("b1 = " + str(parameters["b1"]))print("W2 = " + str(parameters["W2"]))print("b2 = " + str(parameters["b2"]))print("v[\"dW1\"] = " + str(v["dW1"]))print("v[\"db1\"] = " + str(v["db1"]))print("v[\"dW2\"] = " + str(v["dW2"]))print("v[\"db2\"] = " + str(v["db2"]))

W1 = [[ 1.62544598 -0.61290114 -0.52907334] [-1.07347112  0.86450677 -2.30085497]]b1 = [[ 1.74493465] [-0.76027113]]W2 = [[ 0.31930698 -0.24990073  1.4627996 ] [-2.05974396 -0.32173003 -0.38320915] [ 1.13444069 -1.0998786  -0.1713109 ]]b2 = [[-0.87809283] [ 0.04055394] [ 0.58207317]]v["dW1"] = [[-0.11006192  0.11447237  0.09015907] [ 0.05024943  0.09008559 -0.06837279]]v["db1"] = [[-0.01228902] [-0.09357694]]v["dW2"] = [[-0.02678881  0.05303555 -0.06916608] [-0.03967535 -0.06871727 -0.08452056] [-0.06712461 -0.00126646 -0.11173103]]v["db2"] = [[ 0.02344157] [ 0.16598022] [ 0.07420442]]

Expected Output:

W1	[[ 1.62544598 -0.61290114 -0.52907334] [-1.07347112 0.86450677 -2.30085497]]
b1	[[ 1.74493465] [-0.76027113]]
W2	[[ 0.31930698 -0.24990073 1.4627996 ] [-2.05974396 -0.32173003 -0.38320915] [ 1.13444069 -1.0998786 -0.1713109 ]]
b2	[[-0.87809283] [ 0.04055394] [ 0.58207317]]
v["dW1"]	[[-0.11006192 0.11447237 0.09015907] [ 0.05024943 0.09008559 -0.06837279]]
v["db1"]	[[-0.01228902] [-0.09357694]]
v["dW2"]	[[-0.02678881 0.05303555 -0.06916608] [-0.03967535 -0.06871727 -0.08452056] [-0.06712461 -0.00126646 -0.11173103]]
v["db2"]	[[ 0.02344157] [ 0.16598022] [ 0.07420442]]

Note that:

The velocity is initialized with zeros. So the algorithm will take a few iterations to "build up" velocity and start to take bigger steps.

If β=0β=0, then this just becomes standard gradient descent without momentum.

How do you choose ββ?

The larger the momentum ββ is, the smoother the update because the more we take the past gradients into account. But if ββ is too big, it could also smooth out the updates too much.

Common values for ββ range from 0.8 to 0.999. If you don't feel inclined to tune this, β=0.9β=0.9 is often a reasonable default.

Tuning the optimal ββ for your model might need trying several values to see what works best in term of reducing the value of the cost function JJ.

What you should remember:

Momentum takes past gradients into account to smooth out the steps of gradient descent. It can be applied with batch gradient descent, mini-batch gradient descent or stochastic gradient descent.

You have to tune a momentum hyperparameter ββ and a learning rate αα.

4 - Adam

Adam is one of the most effective optimization algorithms for training neural networks. It combines ideas from RMSProp (described in lecture) and Momentum.

How does Adam work?

It calculates an exponentially weighted average of past gradients, and stores it in variables vv (before bias correction) and vcorrectedvcorrected (with bias correction).

It calculates an exponentially weighted average of the squares of the past gradients, and stores it in variables ss (before bias correction) and scorrectedscorrected(with bias correction).

It updates parameters in a direction based on combining information from "1" and "2".

The update rule is, for l=1,...,Ll=1,...,L:

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪vdW[l]=β1vdW[l]+(1−β1)∂J∂W[l]vcorrecteddW[l]=vdW[l]1−(β1)tsdW[l]=β2sdW[l]+(1−β2)(∂J∂W[l])2scorrecteddW[l]=sdW[l]1−(β1)tW[l]=W[l]−αvcorrecteddW[l]scorrecteddW[l]√+ε{vdW[l]=β1vdW[l]+(1−β1)∂J∂W[l]vdW[l]corrected=vdW[l]1−(β1)tsdW[l]=β2sdW[l]+(1−β2)(∂J∂W[l])2sdW[l]corrected=sdW[l]1−(β1)tW[l]=W[l]−αvdW[l]correctedsdW[l]corrected+ε

where:

t counts the number of steps taken of Adam

L is the number of layers

β1β1 and β2β2 are hyperparameters that control the two exponentially weighted averages.

αα is the learning rate

εε is a very small number to avoid dividing by zero

As usual, we will store all parameters in the parameters dictionary

Exercise: Initialize the Adam variables v,sv,s which keep track of the past information.

Instruction: The variables v,sv,s are python dictionaries that need to be initialized with arrays of zeros. Their keys are the same as for grads, that is: for l=1,...,Ll=1,...,L:

v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])s["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])s["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])

In [10]:

# GRADED FUNCTION: initialize_adamdef initialize_adam(parameters) :    """    Initializes v and s as two python dictionaries with:                - keys: "dW1", "db1", ..., "dWL", "dbL"                 - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.        Arguments:    parameters -- python dictionary containing your parameters.                    parameters["W" + str(l)] = Wl                    parameters["b" + str(l)] = bl        Returns:     v -- python dictionary that will contain the exponentially weighted average of the gradient.                    v["dW" + str(l)] = ...                    v["db" + str(l)] = ...    s -- python dictionary that will contain the exponentially weighted average of the squared gradient.                    s["dW" + str(l)] = ...                    s["db" + str(l)] = ...    """        L = len(parameters) // 2 # number of layers in the neural networks    v = {}    s = {}        # Initialize v, s. Input: "parameters". Outputs: "v, s".    for l in range(L):    ### START CODE HERE ### (approx. 4 lines)        v["dW" + str(l+1)] = np.zeros((parameters["W" + str(l+1)].shape))        v["db" + str(l+1)] = np.zeros((parameters["b" + str(l+1)].shape))        s["dW" + str(l+1)] = np.zeros((parameters["W" + str(l+1)].shape))        s["db" + str(l+1)] = np.zeros((parameters["b" + str(l+1)].shape))    ### END CODE HERE ###        return v, s

In [11]:

parameters = initialize_adam_test_case()v, s = initialize_adam(parameters)print("v[\"dW1\"] = " + str(v["dW1"]))print("v[\"db1\"] = " + str(v["db1"]))print("v[\"dW2\"] = " + str(v["dW2"]))print("v[\"db2\"] = " + str(v["db2"]))print("s[\"dW1\"] = " + str(s["dW1"]))print("s[\"db1\"] = " + str(s["db1"]))print("s[\"dW2\"] = " + str(s["dW2"]))print("s[\"db2\"] = " + str(s["db2"]))

v["dW1"] = [[ 0.  0.  0.] [ 0.  0.  0.]]v["db1"] = [[ 0.] [ 0.]]v["dW2"] = [[ 0.  0.  0.] [ 0.  0.  0.] [ 0.  0.  0.]]v["db2"] = [[ 0.] [ 0.] [ 0.]]s["dW1"] = [[ 0.  0.  0.] [ 0.  0.  0.]]s["db1"] = [[ 0.] [ 0.]]s["dW2"] = [[ 0.  0.  0.] [ 0.  0.  0.] [ 0.  0.  0.]]s["db2"] = [[ 0.] [ 0.] [ 0.]]

Expected Output:

v["dW1"]	[[ 0. 0. 0.] [ 0. 0. 0.]]
v["db1"]	[[ 0.] [ 0.]]
v["dW2"]	[[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
v["db2"]	[[ 0.] [ 0.] [ 0.]]
s["dW1"]	[[ 0. 0. 0.] [ 0. 0. 0.]]
s["db1"]	[[ 0.] [ 0.]]
s["dW2"]	[[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
s["db2"]	[[ 0.] [ 0.] [ 0.]]

Exercise: Now, implement the parameters update with Adam. Recall the general update rule is, for l=1,...,Ll=1,...,L:

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪vW[l]=β1vW[l]+(1−β1)∂J∂W[l]vcorrectedW[l]=vW[l]1−(β1)tsW[l]=β2sW[l]+(1−β2)(∂J∂W[l])2scorrectedW[l]=sW[l]1−(β2)tW[l]=W[l]−αvcorrectedW[l]scorrectedW[l]√+ε{vW[l]=β1vW[l]+(1−β1)∂J∂W[l]vW[l]corrected=vW[l]1−(β1)tsW[l]=β2sW[l]+(1−β2)(∂J∂W[l])2sW[l]corrected=sW[l]1−(β2)tW[l]=W[l]−αvW[l]correctedsW[l]corrected+ε

Note that the iterator l starts at 0 in the for loop while the first parameters are W[1]W[1] and b[1]b[1]. You need to shift l to l+1 when coding.

In [15]:

# GRADED FUNCTION: update_parameters_with_adamdef update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,                                beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8):    """    Update parameters using Adam        Arguments:    parameters -- python dictionary containing your parameters:                    parameters['W' + str(l)] = Wl                    parameters['b' + str(l)] = bl    grads -- python dictionary containing your gradients for each parameters:                    grads['dW' + str(l)] = dWl                    grads['db' + str(l)] = dbl    v -- Adam variable, moving average of the first gradient, python dictionary    s -- Adam variable, moving average of the squared gradient, python dictionary    learning_rate -- the learning rate, scalar.    beta1 -- Exponential decay hyperparameter for the first moment estimates     beta2 -- Exponential decay hyperparameter for the second moment estimates     epsilon -- hyperparameter preventing division by zero in Adam updates    Returns:    parameters -- python dictionary containing your updated parameters     v -- Adam variable, moving average of the first gradient, python dictionary    s -- Adam variable, moving average of the squared gradient, python dictionary    """        L = len(parameters) // 2                 # number of layers in the neural networks    v_corrected = {}                         # Initializing first moment estimate, python dictionary    s_corrected = {}                         # Initializing second moment estimate, python dictionary        # Perform Adam update on all parameters    for l in range(L):        # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".        ### START CODE HERE ### (approx. 2 lines)        v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1-beta1) * grads['dW' + str(l+1)]        v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1-beta1) * grads['db' + str(l+1)]        ### END CODE HERE ###        # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".        ### START CODE HERE ### (approx. 2 lines)        v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1 - beta1**t)        v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1 - beta1**t)#                 v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1 - np.exp(beta1, l))#         v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1 - np.exp(beta1, l))        ### END CODE HERE ###        # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".        ### START CODE HERE ### (approx. 2 lines)#         s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1-beta2) * grads['dW' + str(l+1)] * grads['dW' + str(l+1)]#         s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1-beta2) * grads['db' + str(l+1)] * grads['db' + str(l+1)]        s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1 - beta2)*np.power(grads['dW' + str(l+1)],2)        s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1 - beta2)*np.power(grads['db' + str(l+1)],2)        ### END CODE HERE ###        # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".        ### START CODE HERE ### (approx. 2 lines)        s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1 - beta2**2)        s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1 - beta2**2)        ### END CODE HERE ###        # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".        ### START CODE HERE ### (approx. 2 lines)        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v_corrected["dW" + str(l+1)]/(np.power(s_corrected["dW" + str(l+1)],0.5) + epsilon)        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v_corrected["db" + str(l+1)]/(np.power(s_corrected["db" + str(l+1)],0.5) + epsilon)        ### END CODE HERE ###    return parameters, v, s

In [16]:

parameters, grads, v, s = update_parameters_with_adam_test_case()parameters, v, s  = update_parameters_with_adam(parameters, grads, v, s, t = 2)print("W1 = " + str(parameters["W1"]))print("b1 = " + str(parameters["b1"]))print("W2 = " + str(parameters["W2"]))print("b2 = " + str(parameters["b2"]))print("v[\"dW1\"] = " + str(v["dW1"]))print("v[\"db1\"] = " + str(v["db1"]))print("v[\"dW2\"] = " + str(v["dW2"]))print("v[\"db2\"] = " + str(v["db2"]))print("s[\"dW1\"] = " + str(s["dW1"]))print("s[\"db1\"] = " + str(s["db1"]))print("s[\"dW2\"] = " + str(s["dW2"]))print("s[\"db2\"] = " + str(s["db2"]))

W1 = [[ 1.63178673 -0.61919778 -0.53561312] [-1.08040999  0.85796626 -2.29409733]]b1 = [[ 1.75225313] [-0.75376553]]W2 = [[ 0.32648046 -0.25681174  1.46954931] [-2.05269934 -0.31497584 -0.37661299] [ 1.14121081 -1.09244991 -0.16498684]]b2 = [[-0.88529979] [ 0.03477238] [ 0.57537385]]v["dW1"] = [[-0.11006192  0.11447237  0.09015907] [ 0.05024943  0.09008559 -0.06837279]]v["db1"] = [[-0.01228902] [-0.09357694]]v["dW2"] = [[-0.02678881  0.05303555 -0.06916608] [-0.03967535 -0.06871727 -0.08452056] [-0.06712461 -0.00126646 -0.11173103]]v["db2"] = [[ 0.02344157] [ 0.16598022] [ 0.07420442]]s["dW1"] = [[ 0.00121136  0.00131039  0.00081287] [ 0.0002525   0.00081154  0.00046748]]s["db1"] = [[  1.51020075e-05] [  8.75664434e-04]]s["dW2"] = [[  7.17640232e-05   2.81276921e-04   4.78394595e-04] [  1.57413361e-04   4.72206320e-04   7.14372576e-04] [  4.50571368e-04   1.60392066e-07   1.24838242e-03]]s["db2"] = [[  5.49507194e-05] [  2.75494327e-03] [  5.50629536e-04]]

Expected Output:

W1	[[ 1.63178673 -0.61919778 -0.53561312] [-1.08040999 0.85796626 -2.29409733]]
b1	[[ 1.75225313] [-0.75376553]]
W2	[[ 0.32648046 -0.25681174 1.46954931] [-2.05269934 -0.31497584 -0.37661299] [ 1.14121081 -1.09245036 -0.16498684]]
b2	[[-0.88529978] [ 0.03477238] [ 0.57537385]]
v["dW1"]	[[-0.11006192 0.11447237 0.09015907] [ 0.05024943 0.09008559 -0.06837279]]
v["db1"]	[[-0.01228902] [-0.09357694]]
v["dW2"]	[[-0.02678881 0.05303555 -0.06916608] [-0.03967535 -0.06871727 -0.08452056] [-0.06712461 -0.00126646 -0.11173103]]
v["db2"]	[[ 0.02344157] [ 0.16598022] [ 0.07420442]]
s["dW1"]	[[ 0.00121136 0.00131039 0.00081287] [ 0.0002525 0.00081154 0.00046748]]
s["db1"]	[[ 1.51020075e-05] [ 8.75664434e-04]]
s["dW2"]	[[ 7.17640232e-05 2.81276921e-04 4.78394595e-04] [ 1.57413361e-04 4.72206320e-04 7.14372576e-04] [ 4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"]	[[ 5.49507194e-05] [ 2.75494327e-03] [ 5.50629536e-04]]

You now have three working optimization algorithms (mini-batch gradient descent, Momentum, Adam). Let's implement a model with each of these optimizers and observe the difference.

5 - Model with different optimization algorithms

Lets use the following "moons" dataset to test the different optimization methods. (The dataset is named "moons" because the data from each of the two classes looks a bit like a crescent-shaped moon.)

In [17]:

train_X, train_Y = load_dataset()

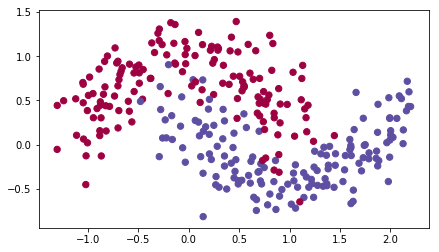
We have already implemented a 3-layer neural network. You will train it with:

Mini-batch Gradient Descent: it will call your function:
- update_parameters_with_gd()

Mini-batch Momentum: it will call your functions:
- initialize_velocity() and update_parameters_with_momentum()

Mini-batch Adam: it will call your functions:
- initialize_adam() and update_parameters_with_adam()

In [18]:

def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,          beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8, num_epochs = 10000, print_cost = True):    """    3-layer neural network model which can be run in different optimizer modes.        Arguments:    X -- input data, of shape (2, number of examples)    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)    layers_dims -- python list, containing the size of each layer    learning_rate -- the learning rate, scalar.    mini_batch_size -- the size of a mini batch    beta -- Momentum hyperparameter    beta1 -- Exponential decay hyperparameter for the past gradients estimates     beta2 -- Exponential decay hyperparameter for the past squared gradients estimates     epsilon -- hyperparameter preventing division by zero in Adam updates    num_epochs -- number of epochs    print_cost -- True to print the cost every 1000 epochs    Returns:    parameters -- python dictionary containing your updated parameters     """    L = len(layers_dims)             # number of layers in the neural networks    costs = []                       # to keep track of the cost    t = 0                            # initializing the counter required for Adam update    seed = 10                        # For grading purposes, so that your "random" minibatches are the same as ours        # Initialize parameters    parameters = initialize_parameters(layers_dims)    # Initialize the optimizer    if optimizer == "gd":        pass # no initialization required for gradient descent    elif optimizer == "momentum":        v = initialize_velocity(parameters)    elif optimizer == "adam":        v, s = initialize_adam(parameters)        # Optimization loop    for i in range(num_epochs):                # Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch        seed = seed + 1        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)        for minibatch in minibatches:            # Select a minibatch            (minibatch_X, minibatch_Y) = minibatch            # Forward propagation            a3, caches = forward_propagation(minibatch_X, parameters)            # Compute cost            cost = compute_cost(a3, minibatch_Y)            # Backward propagation            grads = backward_propagation(minibatch_X, minibatch_Y, caches)            # Update parameters            if optimizer == "gd":                parameters = update_parameters_with_gd(parameters, grads, learning_rate)            elif optimizer == "momentum":                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)            elif optimizer == "adam":                t = t + 1 # Adam counter                parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,                                                               t, learning_rate, beta1, beta2,  epsilon)                # Print the cost every 1000 epoch        if print_cost and i % 1000 == 0:            print ("Cost after epoch %i: %f" %(i, cost))        if print_cost and i % 100 == 0:            costs.append(cost)                    # plot the cost    plt.plot(costs)    plt.ylabel('cost')    plt.xlabel('epochs (per 100)')    plt.title("Learning rate = " + str(learning_rate))    plt.show()    return parameters

You will now run this 3 layer neural network with each of the 3 optimization methods.

5.1 - Mini-batch Gradient descent

Run the following code to see how the model does with mini-batch gradient descent.

In [19]:

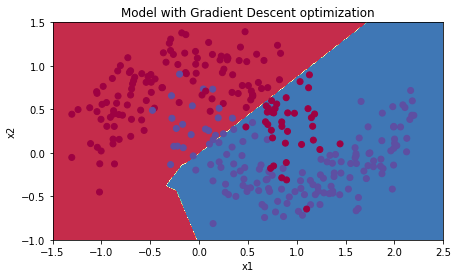
# train 3-layer modellayers_dims = [train_X.shape[0], 5, 2, 1]parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")# Predictpredictions = predict(train_X, train_Y, parameters)# Plot decision boundaryplt.title("Model with Gradient Descent optimization")axes = plt.gca()axes.set_xlim([-1.5,2.5])axes.set_ylim([-1,1.5])plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

Cost after epoch 0: 0.690736Cost after epoch 1000: 0.685273Cost after epoch 2000: 0.647072Cost after epoch 3000: 0.619525Cost after epoch 4000: 0.576584Cost after epoch 5000: 0.607243Cost after epoch 6000: 0.529403Cost after epoch 7000: 0.460768Cost after epoch 8000: 0.465586Cost after epoch 9000: 0.464518

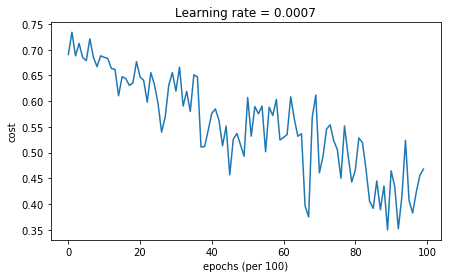
Accuracy: 0.796666666667

5.2 - Mini-batch gradient descent with momentum

Run the following code to see how the model does with momentum. Because this example is relatively simple, the gains from using momemtum are small; but for more complex problems you might see bigger gains.

In [20]:

# train 3-layer modellayers_dims = [train_X.shape[0], 5, 2, 1]parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")# Predictpredictions = predict(train_X, train_Y, parameters)# Plot decision boundaryplt.title("Model with Momentum optimization")axes = plt.gca()axes.set_xlim([-1.5,2.5])axes.set_ylim([-1,1.5])plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

Cost after epoch 0: 0.690741Cost after epoch 1000: 0.685341Cost after epoch 2000: 0.647145Cost after epoch 3000: 0.619594Cost after epoch 4000: 0.576665Cost after epoch 5000: 0.607324Cost after epoch 6000: 0.529476Cost after epoch 7000: 0.460936Cost after epoch 8000: 0.465780Cost after epoch 9000: 0.464740

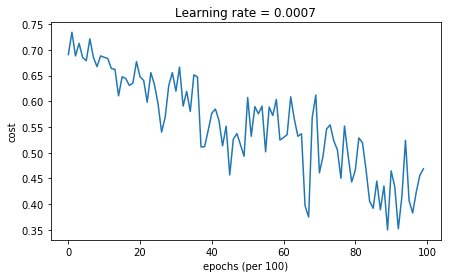
Accuracy: 0.796666666667

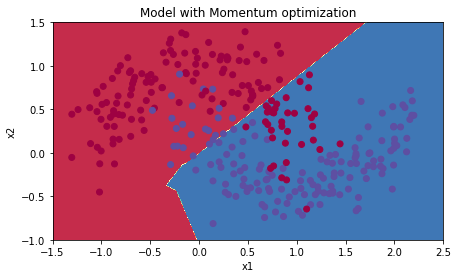
5.3 - Mini-batch with Adam mode

Run the following code to see how the model does with Adam.

In [21]:

# train 3-layer modellayers_dims = [train_X.shape[0], 5, 2, 1]parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")# Predictpredictions = predict(train_X, train_Y, parameters)# Plot decision boundaryplt.title("Model with Adam optimization")axes = plt.gca()axes.set_xlim([-1.5,2.5])axes.set_ylim([-1,1.5])plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

Cost after epoch 0: 0.690563Cost after epoch 1000: 0.651362Cost after epoch 2000: 0.623838Cost after epoch 3000: 0.584447Cost after epoch 4000: 0.539826Cost after epoch 5000: 0.555550Cost after epoch 6000: 0.440262Cost after epoch 7000: 0.329676Cost after epoch 8000: 0.322698Cost after epoch 9000: 0.356201

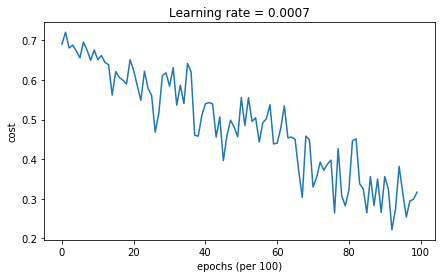
Accuracy: 0.92

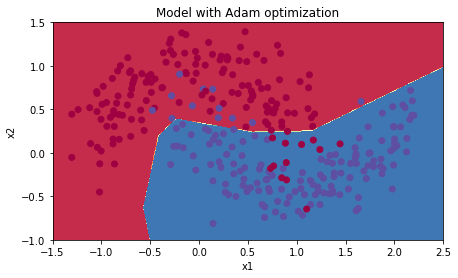
5.4 - Summary

optimization method	accuracy	cost shape
Gradient descent	79.7%	oscillations
Momentum	79.7%	oscillations
Adam	94%	smoother

Momentum usually helps, but given the small learning rate and the simplistic dataset, its impact is almost negligeable. Also, the huge oscillations you see in the cost come from the fact that some minibatches are more difficult thans others for the optimization algorithm.

Adam on the other hand, clearly outperforms mini-batch gradient descent and Momentum. If you run the model for more epochs on this simple dataset, all three methods will lead to very good results. However, you've seen that Adam converges a lot faster.

Some advantages of Adam include: